이번 글에서는 딥러닝에 대한 기본적인 소개와 함께 Dense Layer에 대해 알아보도록 하겠습니다.
Index
1. ANN(Artificial Neural Network)
1.1 Neuron and Artificial Neuron concept
2. Dense Layer
2.1 Data Input
2.2 Computation
2.3 Activation Function
2.4 Next layer
3. Make Class
3.1 Activation class
3.2 Dense class
3.3 Model class
1. ANN(Artificial Neural Network)
딥러닝에 있어 가장 핵심적인 기술인 ANN(인공 신경망)은 신경세포인 Neuron을 추상화 시킨 Artificial Neuron으로 구성된 네트워크 입니다. ANN은 뉴런의 개수가 충분하다면 하나의 은닉층(hidden layer)을 가지고 구하고자 하는 연속 다변수 함수를 근사할 수 있는 universal function approximator으로도 알려져 있습니다.
1.1 Neuron and Artificial Neuron
사람의 뇌에서 가장 기본적인 계산 단위는 뉴런입니다. 뇌 속에는 수많은 (approximately 86 billion neurons) 뉴런으로 이루어진 신경계가 있고 뉴런들을 연결시키는 수많은 시냅스(approximately 10^14 - 10^15 synapses)가 존재합니다.
아래 그림은 생물학적 뉴런(왼쪽)과 이를 수학적으로 모델링한 인공 뉴런입니다.
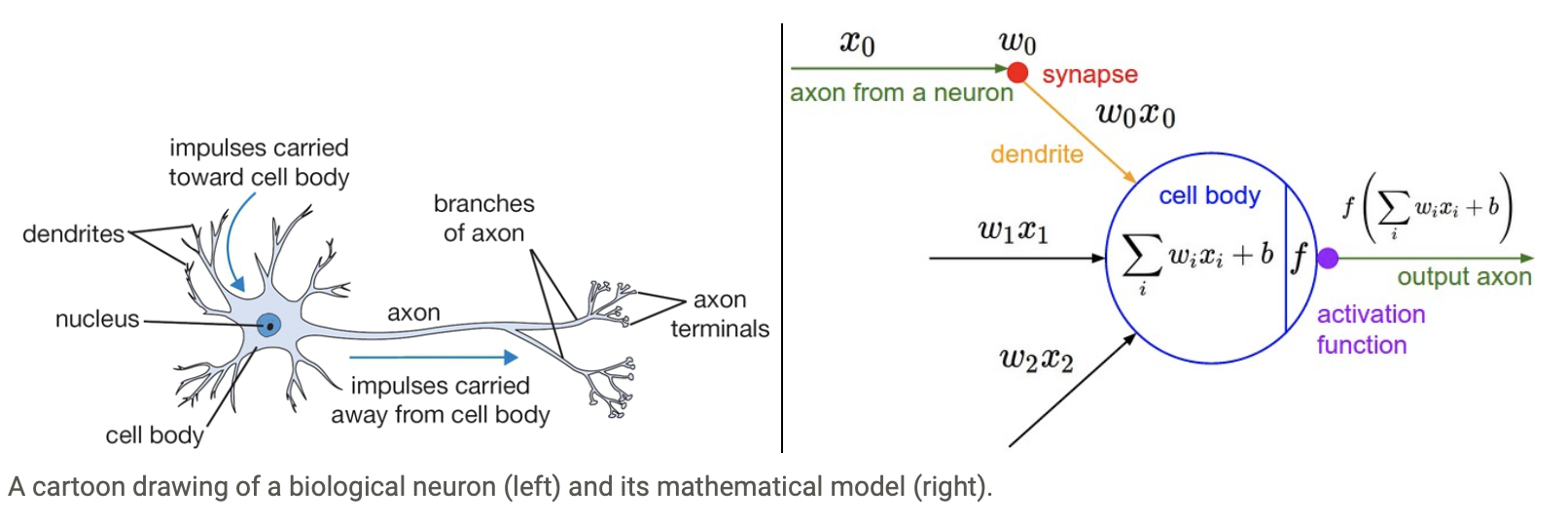
기본적으로 인공 뉴런은
- 수상돌기(Dendrites) : 다른 뉴런의 축삭돌기와 연결되며 Soma라 불리는 몸통에 나뭇가지 형태로 붙어있습니다.
- 축삭돌기(Axon) : 뻗어 나와 다른 뉴런의 수상돌기와 연결됩니다.
- 시냅스(Synapse) : 축삭돌기와 수상돌기가 연결되는 지점입니다.
- 신경세포체(Soma = cell body) : 수상돌기가 모여드는 신경세포의 몸통부분입니다.
하나의 뉴런은 여러 다른 뉴런과 연결되어 있는데 연결되는 시냅스의 강도에 따라 뉴런의 영향력이 결정됩니다.
이러한 영향력이 특정 값을 초과하게 되면 신호가 전달되어 축삭돌기를 통해 다른 뉴런으로 전달 되는 방식입니다.
이 과정을 수학적으로 단순하게 모델링한것이 오른쪽 그림입니다.
n개의 축삭돌기로 들어온 전기적 신호 X를 수학적으로 나타내면 아래와 같이 표현할 수 있습니다.
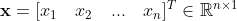
그리고 시냅스의 연결 강도에 따라 갖게되는 뉴런의 영향력은 Weight라고 하는 w 값을 사용하여 아래와 같이 나타낼 수 있습니다.

아래에서 깊게 다뤄볼 Dense Layer는 입력뉴런의 개수에 상관없이 출력의 개수를을 자유롭게 생성할 수 있는데
그 이유는 w 행렬의 colum길이가 해당 은닉레이어의 뉴런의 개수와 같기 때문입니다.

이 개념은 이후 이어질 프로그래밍 구현단계에서 더 상세하게 설명하도록 하겠습니다.
위의 전기적 신호 x 벡터 를 영향력 W 행렬 의 가중치 대로 곱해준뒤 모두 더하는 연산을 cell body에서 진행하게 되는데 이때 아래와 같은 또다른 parameter인 b(bais)벡터까지 더해주게 됩니다.

그 결과 나온 아래와 같은 출력값 z 는 활성함수(Activation Functions)로 입력되고 활성함수는 z값에 따라 최종 output 값을 분류(Classification)하여 output axon으로 전달시키게 되는것 입니다.

여기까지가 ANN의 기본적인 컨셉으로 계속해서 더 심화해 나가 보도록 하겠습니다.
2. Dense Layer
그렇다면 Dense Layer란 무엇일까요?
여기서 '밀집한' 이라는 뜻의 Dense는 애매모호합니다.
이보다 같은 의미로 사용되는 Fully connected Layer가 더 와닿을것 같습니다.
말 그대로 완전 연결되었다(fully connected)라는 것은 아래 그림과 같이
한층의 모든 뉴런이 다음층의 모든 뉴런과 연결된 상태를 의미합니다. 즉, input과 output이 모두 연결되었다는 것입니다.
이때 1번에서 다루었듯이 연결(synapse)사이에는 가중치가 존재하는데 Dense Layer에서는 입력 뉴런과 출력 뉴런의 곱으로
가중치의 수를 바로 구할 수 있습니다.

2.1 data input
이제 기본적인 dense layer의 개념까지 알게되었으니 프로그래밍을 통해 구현해 보도록 하겠습니다.
이에 앞서 1번에서 각 input 뉴런이 가지고 있는 특징을 나타내지 못하는 데이터를 보여 드렸는데
지금부터는 각 input뉴런이 가지고 있는 여러가지 특징을 지정하여 데이터를 생성해 보도록 하겠습니다.
데이터의 특징이란?
지금부터 사용하게 될 "데이터의 특징" 이라는 개념에 대해 서로 다른 임의의 세가지 뉴런을 가정하여 설명 드리도록 하겠습니다.
1번 뉴런의 특징, 색깔: 노란색(0.1)
크기: 2
2번 뉴런의 특징, 색깔: 파란색(0.2)
크기: 3
3번 뉴런의 특징, 색깔: 붉은색(0.3)
크기: 4
위의 데이터를 [row= 특징 , col=뉴런의 번호] 를 가지는 행렬로 나타내면 아래와 같습니다.

데이터의 특징에 대해 이해하였으니 특징을 지니는 데이터를 생성 해 보도록 하겠습니다.
import numpy as np
N, n_feature, n_neuron = 16, 5, 4
# N = number of input neurons
# input neurons data
X = normal(0, 1, (n_feature, N)) # (5, 16)5가지 특징을 지니는 16개의 Input neurons를 생성하였습니다.
여기서 n_neuron은 Dense Layer의 output neurons의 개수를 의미합니다.
그럼 이것을 활용하여 w(가중치)와 b(bais)를 설정 해 주도록 하겠습니다.
W = normal(0, 1, (n_feature, n_neuron)) # (5, 4)
B = normal(0, 1, (n_neuron, 1)) # (4, 1)
2.2 Computation
다음은 앞서 말씀드린 Soma(cell body)에서
X.transpose행렬에 W행렬을 numpy.matmul 과 이후 B.transpose값을 broadcasting하며 더해주는 연산을 진행시키도록 하겠습니다.
여기서 행과 열이 곱해지는 위치를 아래와 같이 잘 염두해야 합니다.
왜냐하면 X를 transpose해주지 않으면 행렬연산이 되지 않기 때문입니다. B또한 마찬가지 입니다.
(numpy의 tensor연산에 대해 잘 생각해보아야 합니다.)
Z = (X.T @ W + B.T).T2.3 Activation Function
마지막으로 Z값을 Activation Function에 대입하여 output값인 A를 얻어보도록 하겠습니다.
저는 simoid function을 사용했습니다.
A = 1/(1 + np.exp(-Z))
2.4 Next Layer
그럼 dense layer를 하나 더 깔아줄 순 없을까요?
당연히 대답은 yes 입니다.
아주 간단하게도 위와 같은 과정을 아래와 같이 숫자만 바꿔 한번 더 만들어 주면 됩니다.
n_neuron2 = 30
W2 = normal(0, 1, (n_neuron, n_neuron2)) # (4, 30)
B2 = normal(0, 1, (n_neuron2, 1)) # (30, 1)
print(A.shape, W2.shape, B2.shape)
Z2 = (A.T @ W2 + B2.T).T # (n_neuron2, 16)
A2 = 1/(1 + np.exp(-Z2)) # (n_neuron2, 16)
이로써 간단한 input data를 통해 2층의 dense layer를 통과하여 output A2 를 생성하는 과정을 연습해 보았습니다.
3. Make Class
이제 위와 같은 과정을 Class화 하여 활용성 있는 코드를 짜보도록 하겠습니다.
어떻게 구성할지 스케치부터 해볼까요?
import numpy as np
# For forward propagation, we should make Dense class.
# The reason of making Activation class seperately is to use it flexibly in another class.
# Model class make multiple Dense Class. They can have different Activation functions.
class Activation:
pass
class Dense:
pass
class Model:
passForward propagation을 구현하기 위해서는 Dense layer를 구성하는 class 가 필요합니다.
클린코드를 작성하기 위해 Activation class 를 따로 구성해 주는게 좋을것 같습니다.
그리고 여러 Dense layer로 이루어진 Model을 구성하기 위해 Model class를 만들어 마무리 짓도록 하겠습니다.
3.1 Activation class
초기화를 위한 __init__ 함수와 activation함수에 따른 결과값을 return하는 call 함수를 만들어 보았습니다.
class Activation:
def __init__(self,activation='sigmoid'):
self.activation = activation
def __call__(self,x):
if self.activation == 'sigmoid':
y = 1/(1+np.exp(-x))
elif self.activation =='tanh':
y = (np.exp(x)-np.exp(-x)) / ((np.exp(x)+np.exp(-x))
elif self.activation =='softmax':
y = np.exp(x) / np.sum((np.exp(x))
else:
print("UNKOWN activation")
return y3.2 Dense Class
1. layer마다 neuron의 개수와 Activation function이 다를 수 있기 때문에 초기화 해줍니다.
2. parameter를 초기화 해주는 함수를 만든뒤 Input data의 feature값을 weight의 row로, neuron의 개수를 column으로 설정합니다.
3. call 함수는 Inputdata를 받아와 연산 후 변수 Z에 담아줍니다.
4. Activation class의 input값으로 Z를 넣기 위해 self.activation(Z) 를 이용하여 변수 A에 담아준 뒤 A.T값을 return해줍니다.
(A를 transpose하는 이유는 다음 layer에서 input값으로 작용하기 때문입니다.)
class Dense:
# 각 layer마다 초기화 해야하는 값 1.neuron의 개수 2.Activation Function
def __init__(self,neuron,activation='sigmoid'):
self.neuron = neuron
self.activation = Activation(activation)
def _init_params(self,x):
n_feature = x.shape[0] #n_feature = x_feature
self.W = np.random.normal(n_feature,self.neuron)
self.B = np.random.normal(self.neuron,1)
def __call__(self,x):
if len(self.W) == 0:
self._init_params(x)
Z = x.T @ self.W + self.B.T
A = self.activation(Z)
return A.T



