이번 글부터는 Backpropagation에서 Gradient-based Learning을 하는 이유에 대해 알아보도록 하겠습니다.
Index
1. CNN, Forward propagation review
2. Gradient-based Learning
1. CNN , FC(Dense) layer , Convolution layer
Back propagation을 위해 간단히 Forward propagation을 Review하는 시간을 갖도록 하겠습니다.
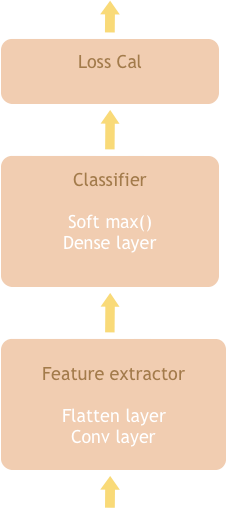
1.1 Feature Extractor
CNN(Convolution Neural Network)은 입력받은 데이터를 Feature Extractor에서 특징을 추출하는 과정을 갖습니다. 이 단계에서 Convolution layer는 불필요한 데이터를 filtering해주지만 형상을 유지하기 때문에 flatten과정을 거친 뒤 Classifier로 넘어가게 됩니다.
1.2 Classifier
받아온 1차원 데이터는 Dense layer (FC(Fully Connected) layer)를 거친 후
soft max함수를 통해 0~1 값의 확률을 반환하여 classification을 완료합니다.
1.3 Loss Calculator
마지막으로 loss claculator에서는 예측값된 값과 실제 값의 오차를 연산합니다.
이때 우리가 정답을 알기 위해서는 예측값과 실제 정답 사이의 오차를 줄여 나가야겠죠?
그 과정이 바로 Back propagation에서 일어나게 됩니다.
지금부터 Back propagation이 어떻게 진행되는지 차근차근 알아가 보도록 하겠습니다.
2. Gradient-based Learning
Back propagation은 CNN이 직접 오차를 줄여 나가기 위해 본격적인 학습을 시작하는 단계입니다.
이를 위해서 가장 기본이 되는 Gradient-based Learning이 필요합니다.
그렇다면 Gradient-based Learning이 무엇을 의미할까요?
우리는 순전파 과정에서 나온 SE(squared error)를 줄여나가는 방법을 이용할것입니다. SE는 2차 함수라는것을 알고있고 이 값이 최소가 되는값은 w에 대한 미분값이 0이 되는 값을 의미합니다. 이를 이용하여 우리는 최초 설정된 임의의 w(weight),b(bais)값을 업데이트 시킬것입니다. 이들을 update하는 방법으로 SE를 w에 대해 편미분한 값을 기존 w에서 빼주는 방법을 이용하게 됩니다.
이때 편미분값에 특별한 계수를 곱해주게 됩니다. 왜냐하면 일정한 방향으로 감소해야하는데 오히려 발산하게 될 수 있기 때문입니다.
이해를 돕기 위해 간단한 코드를 통해 설명하도록 하겠습니다.
import numpy as np
import matplotlib.pyplot as plt
#x값 , 계수, y값 설정
x = np.linspace(-4,4,100)
coeff = 1.2
y = coeff*(x**2)
fig, ax = plt.subplots(figsize=(20,10))
ax.plot(x,y)
x = 3
for _ in range(5):
y = coeff*(x**2)
ax.scatter(x,y, color='red', s =100)
#y값 미분
diff = 2*coeff*x
# 업데이트 되는 값들 찍어주기
x_next = x- diff
y_next = coeff*(x_next**2)
ax.plot([x,x_next],[y,y_next],color ='red')
x = x_next
ax.tick_params(labelsize=20)
ax.grid()
plt.show()
위의 코드는 계수 없이 기존값에 미분값을 빼준 $x=:x-f'(x)$의 형태를 나타내고 시각화한 코드입니다.
이 경우 아래 그림과 같이 발산하게 되어 0을 찾아 가지 못하게 됩니다.
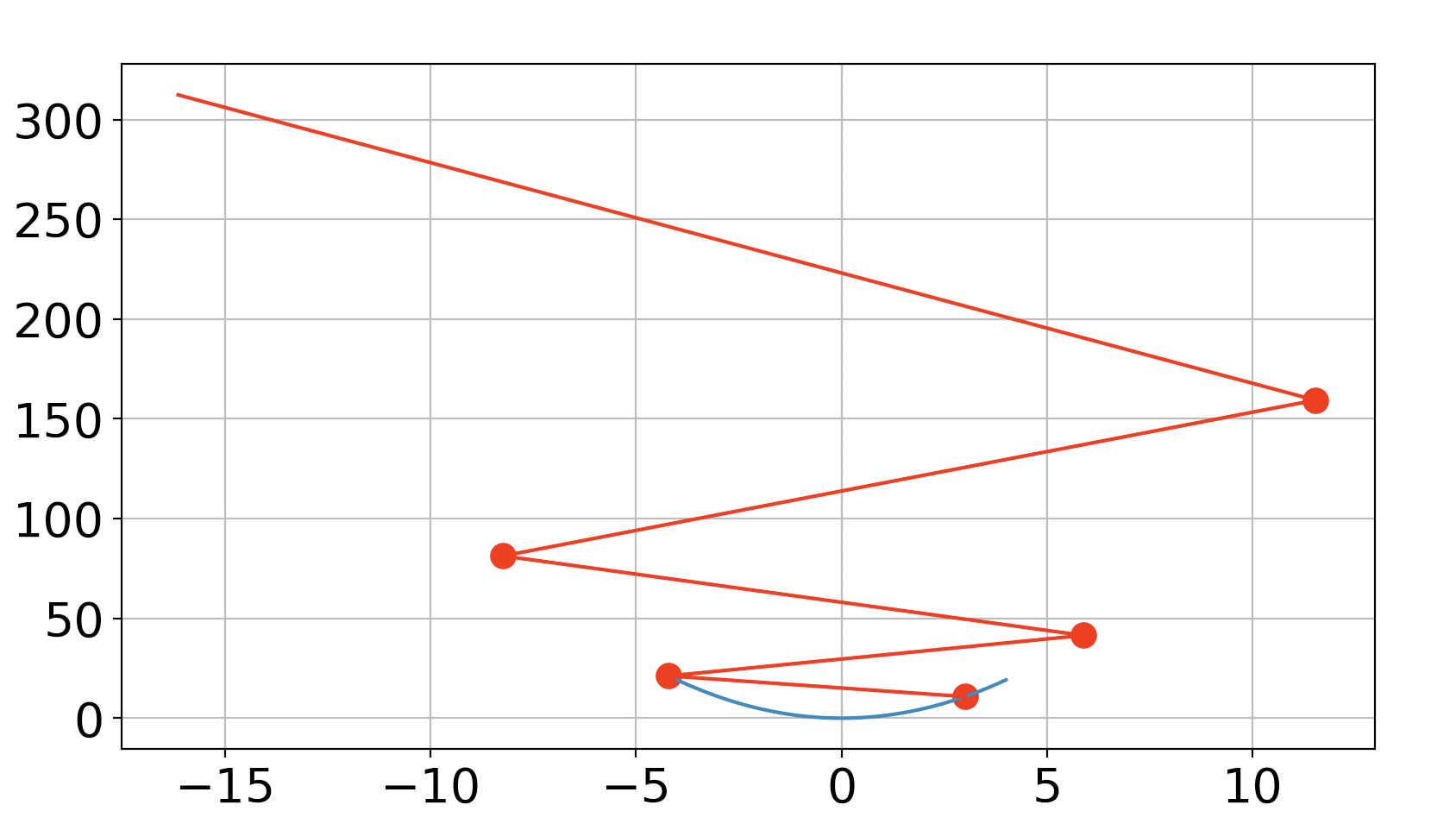
이 같은 상황을 방지하고자 우리는 lr(Learning Rate)이라는 계수를 추가하여 한 방향으로 감소하도록 조정 해 주도록 하겠습니다.
import numpy as np
import matplotlib.pyplot as plt
#x값 , 계수, y값 설정
x = np.linspace(-4,4,100)
coeff = 1.2
y = coeff*(x**2)
lr = 0.2
fig, ax = plt.subplots(figsize=(20,10))
ax.plot(x,y)
x = 3
for _ in range(5):
y = coeff*(x**2)
ax.scatter(x,y, color='red', s =100)
#y값 미분
diff = 2*coeff*x
# 업데이트 되는 값들 찍어주기
x_next = x- lr*diff
y_next = coeff*(x_next**2)
ax.plot([x,x_next],[y,y_next],color ='red')
x = x_next
ax.tick_params(labelsize=20)
ax.grid()
plt.show()그 결과 아래와 같이 우리가 원하는 값을 향해가는 모습을 확인할 수 있습니다.
수식으로 표현하면 $x=:x-LearningRate*f'(x)$ 가 될것입니다.

우리는 이와 같은 방법을 간단한 역전파 과정을 통해 확인 해 볼 수도 있습니다.
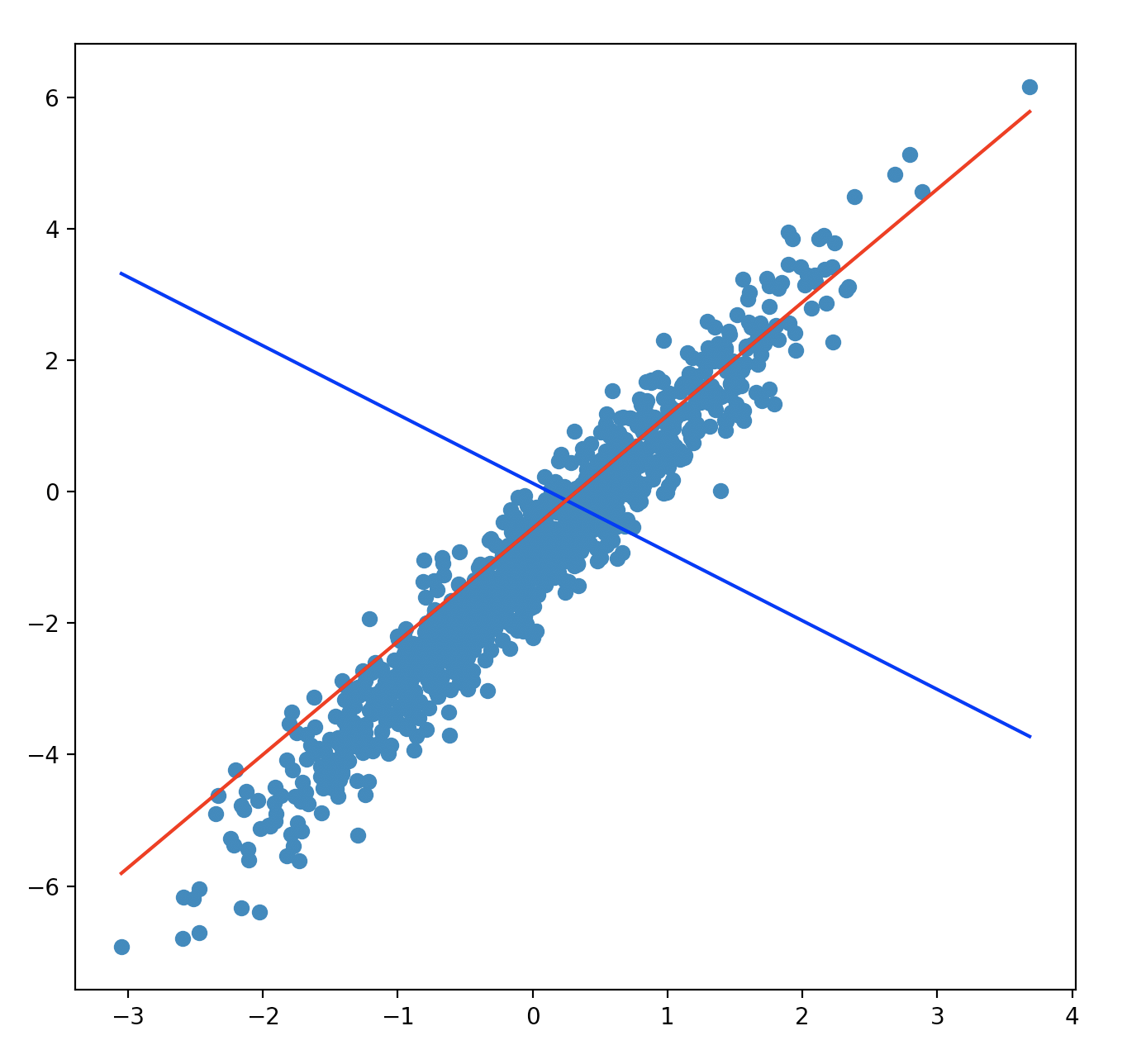
아래는 노이즈가 있는 임의의 데이터셋을 만든 뒤
처음 예측한 직선이 30 epochs를 통해 점차적으로 데이터셋을 예측해 나가도록 모델링한 코드입니다.
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
epochs, lr = 30, 0.3
####make dataset####
a, b = 2, -1
noise_factor = 0.5
X = np.random.randn(1000, 1)
Y = a*X + b + noise_factor * np.random.randn(1000, 1)
fig, ax = plt.subplots(figsize=(10, 10))
ax.scatter(X, Y)
##임의의 w,b설정##
w, b = np.random.randn(1), np.random.randn(1)
##min,max를 이용해 데이터셋X에 대한 예측
x_min, x_max = np.min(X), np.max(X)
x_predictor = np.linspace(x_min, x_max, 2)
y_predictor = w*x_predictor + b
ax.plot(x_predictor, y_predictor, 'blue')
for epoch in range(epochs):
for x, y in zip(X, Y):
pred = x * w + b
loss = (pred - y)**2
##diff
dloss_dpred = 2*(pred - y)
dpred_dw, dpred_db = x, 1
#chain rule
dloss_dw = dloss_dpred * dpred_dw
dloss_db = dloss_dpred * dpred_db
#조정된 값
w = w - lr * dloss_dw
b = b - lr * dloss_db
#조정된값에 의한 최종값
y_predictor = w*x_predictor + b
ax.plot(x_predictor, y_predictor, 'red')
plt.show()아래의 그림에서는 최초 파란선이 학습을 통해 빨간선으로 예측해 내고 있는것을 보여줍니다.
여기서 중요한 포인트는 조정된값 w = w - lr * dloss_dw 라는것 입니다. (dloss_dw는 loss함수를 w로 편미분한 값을 의미합니다)
우리는 lr을 설정 해 줌으로써 발산하지 않고 오차를 줄여나가는 방향으로 인도할 수 있게 됩니다.